Lecture 6 – Clustering K-Means, K-Medoids, Hierarchical & DBSCAN

Lecture 6 explains clustering in Data Mining, including K-Means, K-Medoids, hierarchical clustering, and DBSCAN with diagrams, algorithms, examples, Python code, real-world applications, and comparisons for BS CS, BS AI, BS IT & Data Science students.

Clustering is one of the most fundamental techniques in unsupervised learning. Unlike supervised models that rely on labeled datasets, clustering finds natural groups within data without prior knowledge of categories. Whether it’s grouping customers, identifying abnormal behavior, segmenting images, or analyzing biological data, clustering algorithms are used everywhere.

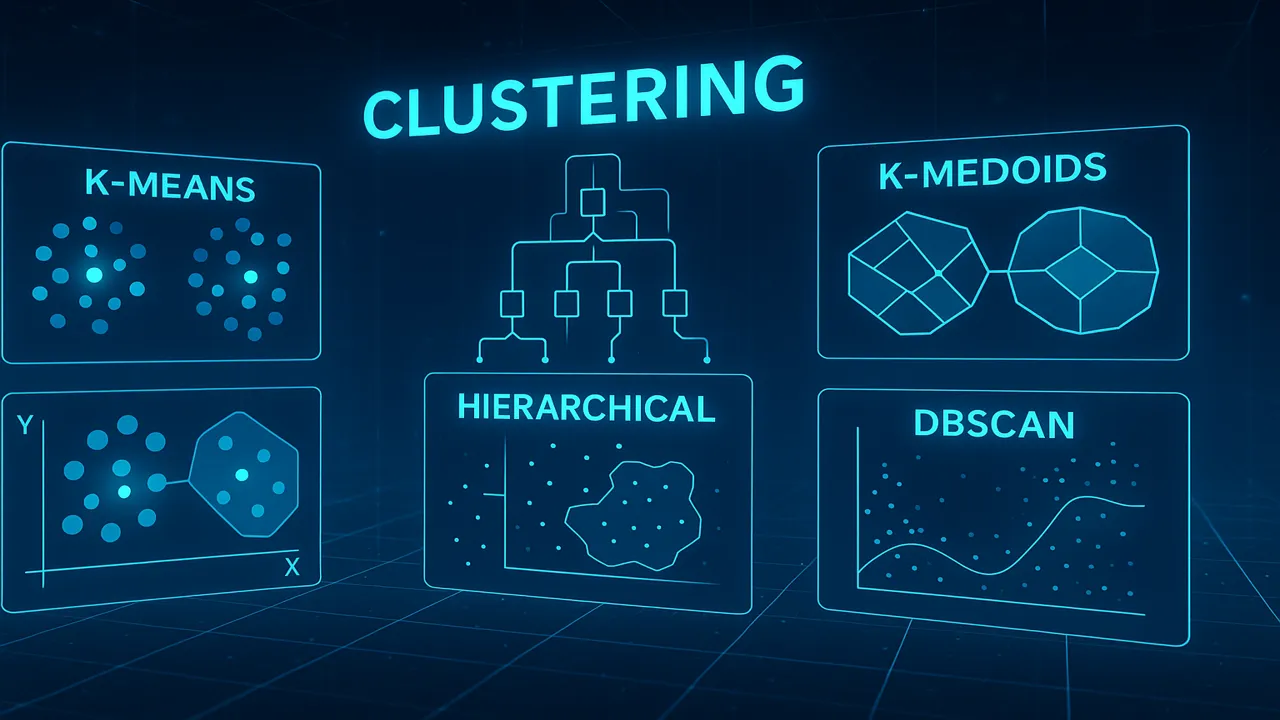
This lecture dives deep into the four most important clustering algorithms:

• K-Means
• K-Medoids
• Hierarchical Clustering
• DBSCAN

You will learn how they work, when to use them, their strengths, weaknesses, and real-world scenarios.

Introduction to Clustering

What Is Clustering?

Clustering is the process of grouping data points based on similarity.

Each group is called a cluster.

Examples:

• Grouping customers by behavior
• Grouping documents by similarity
• Grouping images by features

Why Use Clustering?

• Discover hidden structures
• Reduce data complexity
• Improve decision-making
• Preprocessing step for other algorithms

Clustering vs Classification

Classification	Clustering
Labeled data	Unlabeled data
Predict categories	Discover groups
Supervised	Unsupervised
Used for known outcomes	Used for exploration

Types of Clustering Methods

Clustering algorithms are divided into three main families.

1. Partitioning Methods

They divide data into K clusters:

• K-Means
• K-Medoids

2. Hierarchical Methods

They build a tree of clusters:

• Agglomerative
• Divisive

3. Density-Based Methods

They find clusters of arbitrary shapes:

• DBSCAN
• OPTICS

K-Means Clustering

K-Means is the most famous clustering algorithm.

How K-Means Works (Step-by-Step)

1. Choose the number of clusters K
2. Randomly select K centroids
3. Assign each data point to the nearest centroid
4. Update centroids (mean of assigned points)
5. Repeat until convergence

Distance Metrics

Common metrics:

• Euclidean distance
• Manhattan distance

Euclidean formula:

d = √((x1 - x2)² + (y1 - y2)²)

Choosing K (Elbow Method)

Plot:

K vs. Inertia (Within-cluster sum

Look for the “elbow” the point where improvement slows.

Advantages of K-Means

Fast
Easy to understand
Works well with large datasets

Limitations

Requires K
Sensitive to outliers
Only works well with spherical clusters

Numeric Example (Simple Demonstration)

Dataset:

Points: (1,1), (2,1), (4,3), (5,4)
K = 2

Initial centroids:

C1 = (1,1)
C2 = (5,4)

Clusters form as:

Cluster A: (1,1), (2,1)
Cluster B: (4,3), (5,4)

Centroids update:

New C1 = (1.5,1)
New C2 = (4.5,3.5)

Repeat until stable.

Machine Learning Course

K-Medoids (PAM Algorithm)

K-Medoids is similar to K-Means but more robust to noise.

Difference from K-Means

K-Means	K-Medoids
Uses mean	Uses medoid (actual data point)
Sensitive to outliers	Robust to outliers

PAM Algorithm Steps

1. Choose K points as medoids
2. Assign each data point to the nearest medoid
3. Swap medoids with non-medoids to reduce cost
4. Continue until no improvement

When to Use K-Medoids

• When dataset contains noise
• When outliers may distort centroids
• When you need guaranteed actual data representatives

scikit-learn documentation

Hierarchical Clustering

Hierarchical clustering builds a tree-like structure called a dendrogram.

Two Types

1. Agglomerative

Starts with each point as its own cluster, then merges clusters.

2. Divisive

Starts with one cluster, then splits into smaller clusters.

Dendrogram Explanation

      ┌──────────── A
   ┌──┤
   │  └──────────── B
───┤
   │   ┌────────── C
   └───┤
       └────────── D

Cutting the dendrogram at different heights gives different numbers of clusters.

DBSCAN (Density-Based Clustering)

DBSCAN is powerful for discovering clusters of any shape.

Key Concepts

• Core Point: Enough neighbors
• Border Point: Near a core
• Noise Point: Irregular/outlier

How DBSCAN Works

1. Choose parameters:
   • ε (epsilon) → distance
   • minPts → minimum neighbors
2. Find core points
3. Form clusters around them
4. Mark remaining points as noise

Advantages of DBSCAN

Finds arbitrarily shaped clusters
Handles noise
No need to specify K

Limitations

Difficult to choose ε
Struggles with varying density

Comparison Table of Clustering Algorithms

Algorithm	Needs K?	Handles Noise	Cluster Shape	Speed
K-Means	Yes	Poor	Spherical	Fast
K-Medoids	Yes	Good	Spherical	Medium
Hierarchical	No	Medium	Tree structure	Slow
DBSCAN	No	Excellent	Arbitrary	Medium

Practical Case Studies

1. Customer Segmentation

K-Means is commonly used to group customers based on:

• Spending habits
• Demographics
• Browsing behavior

2. Image Segmentation

Hierarchical clustering groups similar pixels.

3. Fraud Detection

DBSCAN identifies abnormal transactions as noise.

Python Code Examples

K-Means

from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
labels = kmeans.labels_

K-Medoids

from sklearn_extra.cluster import KMedoids

model = KMedoids(n_clusters=3)
model.fit(X)

Hierarchical

from sklearn.cluster import AgglomerativeClustering

hier = AgglomerativeClustering(n_clusters=3)
hier.fit(X)

DBSCAN

from sklearn.cluster import DBSCAN

db = DBSCAN(eps=0.5, min_samples=5)
db.fit(X)

Common Mistakes in Clustering

• Using K-Means without scaling data
• Choosing wrong K
• Using K-Means for non-spherical clusters
• Misinterpreting dendrograms
• Incorrect DBSCAN parameter selection

Summary

Lecture 6 covered four primary clustering methods used in Data Mining: K-Means, K-Medoids, Hierarchical Clustering, and DBSCAN. You learned how each algorithm works, the mathematics behind them, their real-world applications, strengths, limitations, and Python implementations. These clustering techniques form the backbone of unsupervised learning.

Next. Lecture 7 Outlier & Anomaly Detection in Data Mining

People also ask: