Analysis of Algorithms – Example of Summing Natural Numbers

This educational graphic demonstrates two approaches to solving the sum of natural numbers problem a direct formula and a loop-based algorithm as part of the Analysis of Algorithms topic.

Introduction

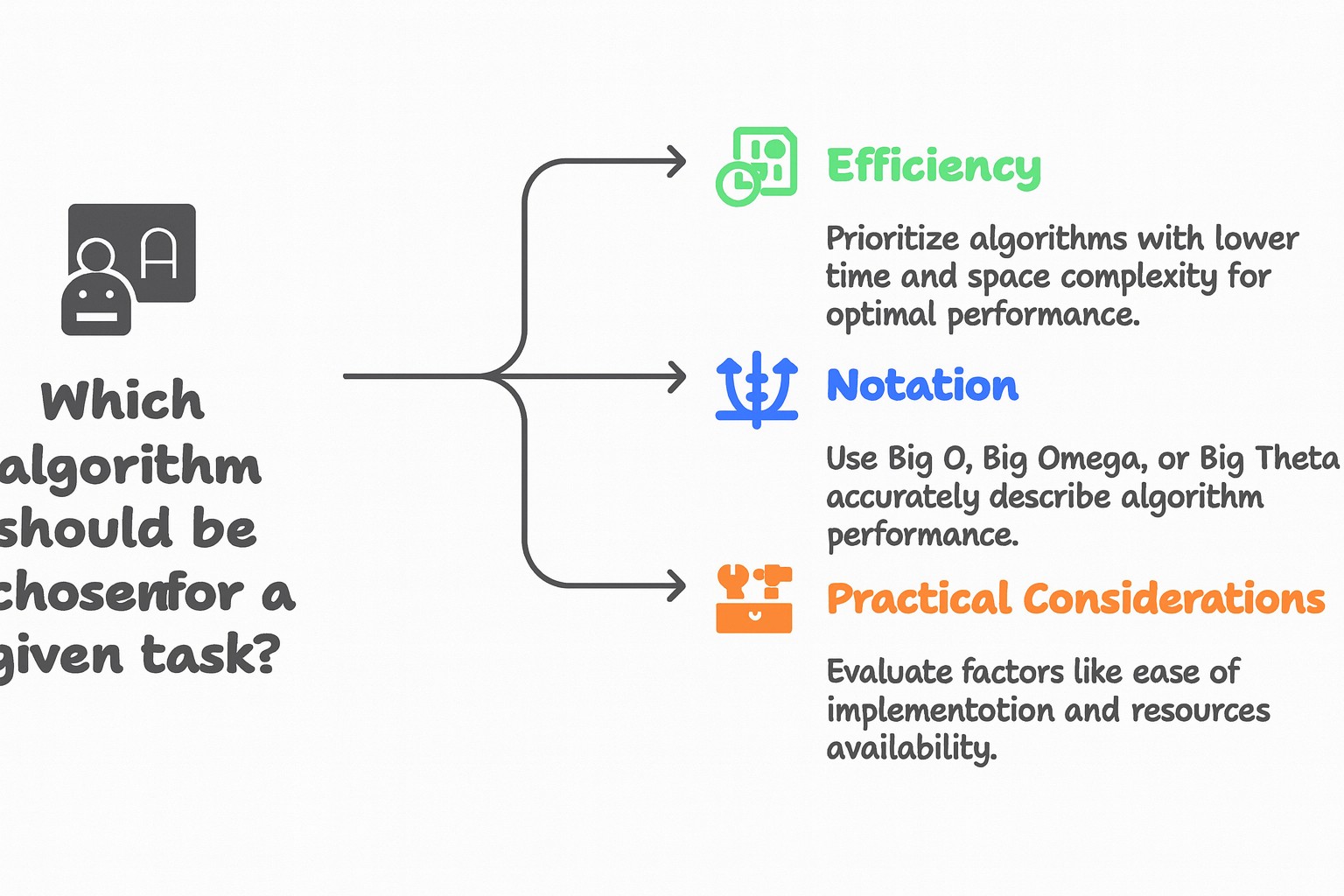
An Algorithm is a set of instructions to perform a task or to solve a given problem.
There are several different algorithms to solve a given problem.
Analysis of algorithm deals in finding the best algorithm which runs fast and takes less memory.

Example:
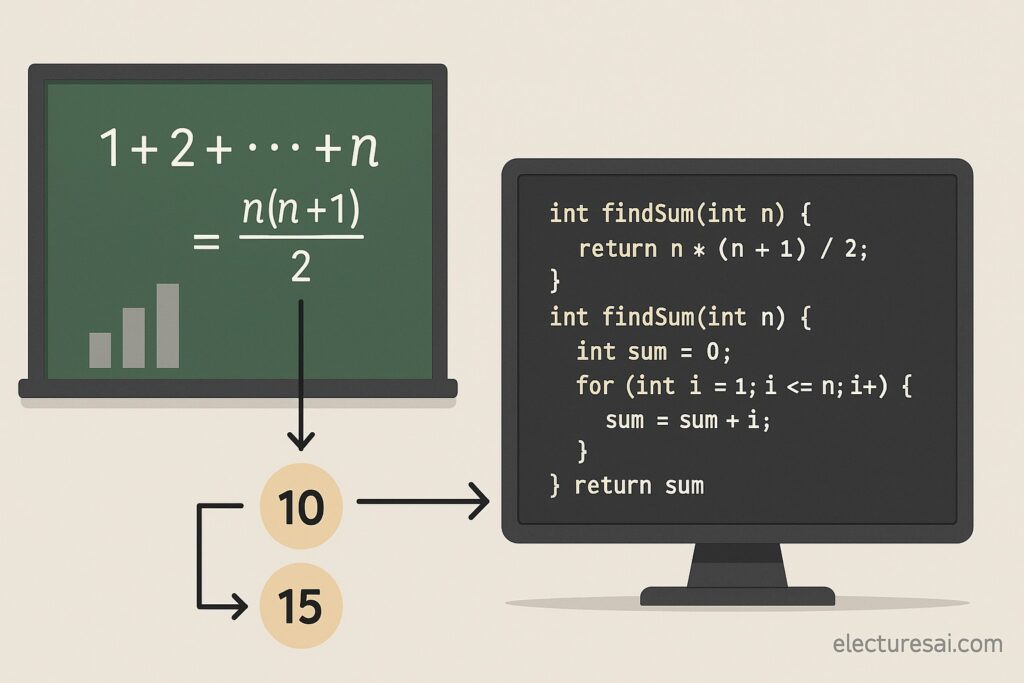
Find the sum of first n natural numbers.

• Input: n = 4 → Output: 10 (1 + 2 + 3 + 4)
• Input: n = 5 → Output: 15 (1 + 2 + 3 + 4 + 5)

// Azhar
int findSum(int n) {
    return n * (n + 1) / 2;
}

// Ahsan
int findSum(int n) {
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

Explore fundamental programming concepts and data management methods in: Introduction to Data Structures 2025

Time Complexity

Time complexity is the amount of time taken by an algorithm to run.
The input processed by an algorithm helps in determining the time complexity.

// Azhar
int findSum(int n) {
    return n * (n + 1) / 2;
}

// Ahsan
int findSum(int n) {
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

Understand the evolution of cybersecurity: History of Cybersecurity

Space Complexity

Space complexity is the amount of memory or space taken by an algorithm to run.
The memory required to process the input helps determine the space complexity.

// Azhar
int findSum(int n) {
    return n * (n + 1) / 2;
}

// Ahsan
int findSum(int n) {
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

Learn how logic circuits form the base of computer architecture in our detailed post: Digital Logic Design – Number Systems

Complexity Function

1, 2, 8: Once
3, 4, 5, 6, 7: Once per each iteration of for loop (N iterations)

Total: 5N + 3

Complexity Function: f(N) = 5N + 3

Growth of 5N + 3

Estimated Running Time for Different N Values:

N	Steps
10	53
100	503
1,000	5,003
1,000,000	5,000,003

As N grows, the number of steps grows in linear proportion to N for this “Sum” function.

or a deeper look into how modern algorithms empower autonomous systems, check out our latest post: Agentic AI in Research – Latest Developments 2025

Asymptotic Analysis

• Asymptotic analysis helps in evaluating performance of an algorithm in terms of input size and its increase.

• Using asymptotic analysis we don’t measure actual running time of algorithm.

• It helps in determining how time and space taken by algorithm increases with input size.

Asymptotic Notations

Asymptotic notations describe running time of an algorithm in terms of input size.

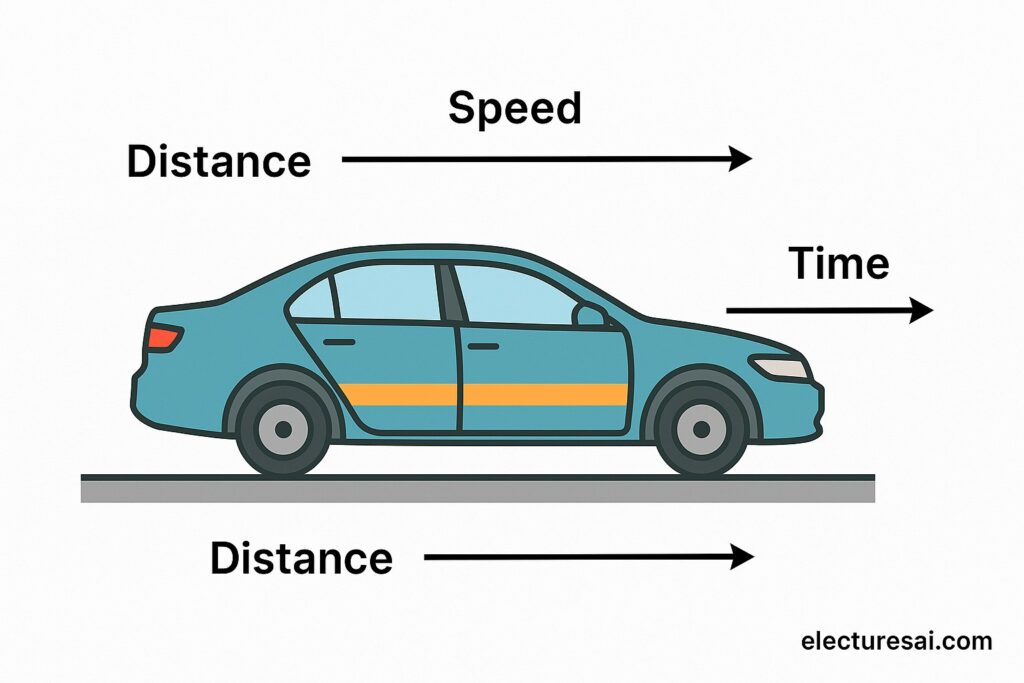
Example:
Performance of a car in 1 litre of petrol

• Highway (min traffic): 25 km/litre
• City (max traffic): 15 km/litre
• Average traffic: 20 km/litre

They help determine:

1. Best Case
2. Average Case
3. Worst Case

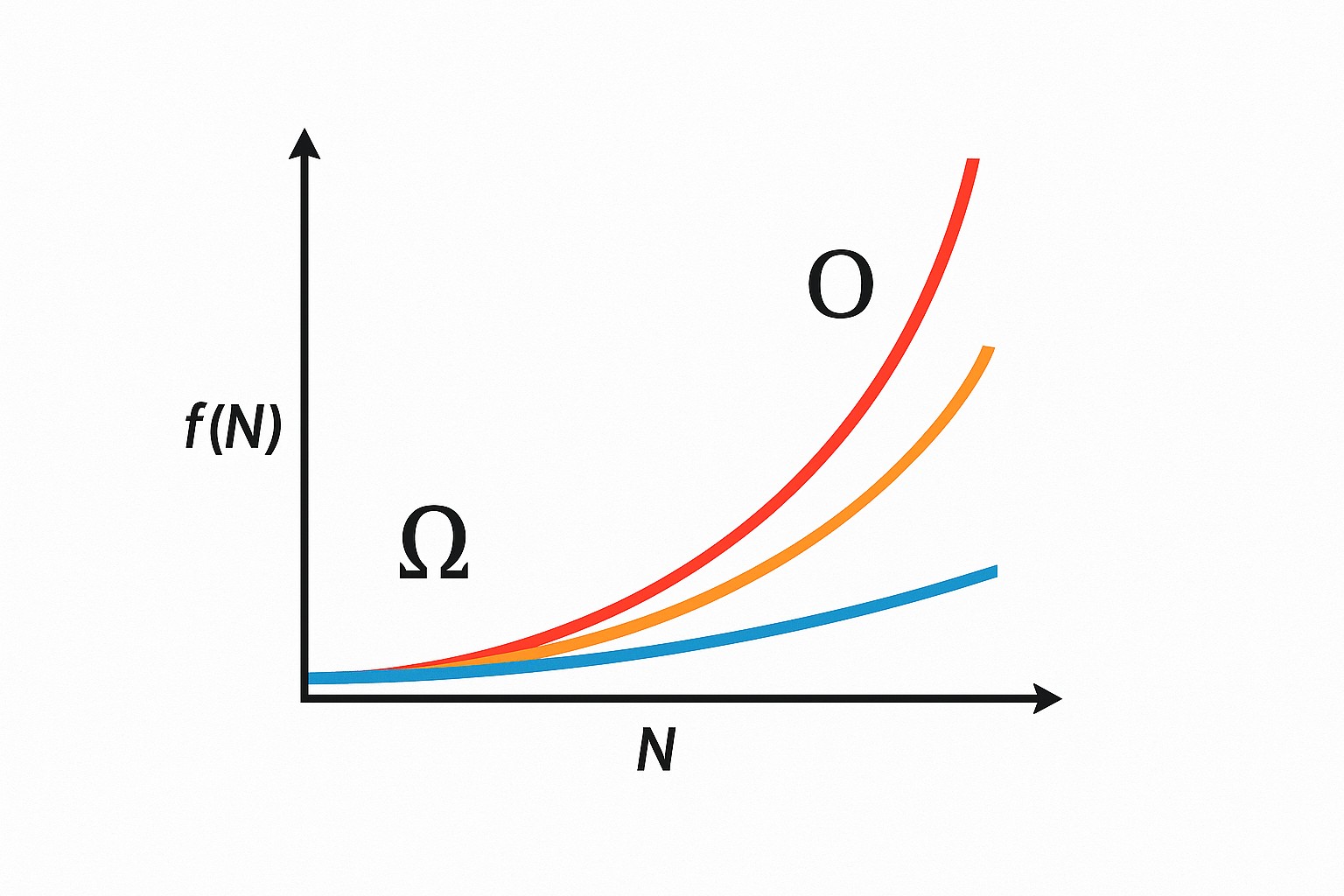
Types of Asymptotic Notations

Omega (Ω) Notation

• Expresses the lower bound of an algorithm’s running time.
• Lower bound means minimum time an algorithm takes to complete.

Example:
If an algorithm takes 100 seconds as best case time, 100 seconds is its lower bound.

Big O (O) Notation

• Expresses the upper bound of an algorithm’s running time.
• Upper bound means maximum time an algorithm can take to complete.

Example:
If it takes 100 seconds as worst case, 100 seconds is its upper bound.

Theta (Θ) Notation

• Represents both upper and lower bounds of an algorithm’s running time.
• Indicates the average amount of time the algorithm takes to complete.

Example:
If it runs 100 s first time, 120 s second, 110 s third, Theta notation gives the average.

Conclusion

Analysis of algorithms is essential for understanding efficiency in programming.
By studying time and space complexity using asymptotic analysis, developers can select the most optimal solution.

People also ask: