Arithmetic sequences, their formulas, properties, and real-life examples. Includes nth term, sum of n terms, and difference explanation.
Introduction to Arithmetic Sequence
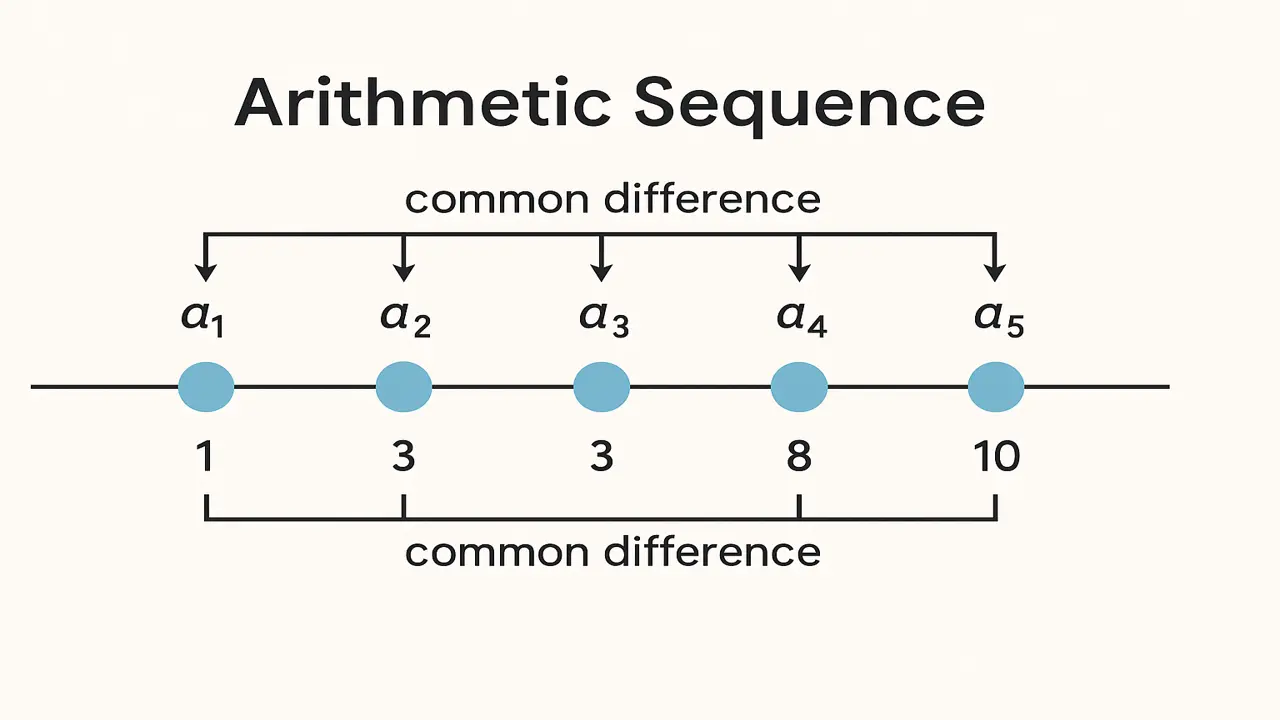
An Arithmetic Sequence (A.P.) is a sequence of numbers in which the difference between consecutive terms remains constant.
This constant difference is called the common difference (d).
For example:
2, 4, 6, 8, 10, … forms an arithmetic sequence with common difference d = 2.
In general form, an arithmetic sequence can be written as:
a, a + d, a + 2d, a + 3d, …
Where:
- a = first term
- d = common difference
- n = number of terms
Arithmetic sequences are widely used in mathematics, finance, physics, and everyday reasoning to represent linear growth or decay.
General Term (nth Term) of an Arithmetic Sequence
The nth term of an arithmetic sequence is given by the formula: an=a+(n−1)da_n = a + (n – 1)dan=a+(n−1)d
Where:
- an = nth term
- a = first term
- d = common difference
- n = number of terms
Example 1:
Find the 10th term of the sequence: 3, 6, 9, 12, …
Here,
a=3,d=3,n=10a = 3, d = 3, n = 10a=3,d=3,n=10 a10=3+(10−1)×3=30a_{10} = 3 + (10 – 1) \times 3 = 30a10=3+(10−1)×3=30
10th term = 30
Sum of n Terms of an Arithmetic Sequence
The sum of the first n terms of an arithmetic sequence is given by:
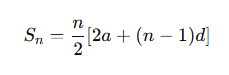
Alternatively, if you know the first and last terms (a and l):
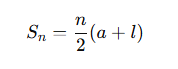
Where:
- Sn = sum of first n terms
- a = first term
- l = last term
- d = common difference
Example 2:
Find the sum of the first 10 terms of 2, 5, 8, 11, …
Here, a=2,d=3,n=10
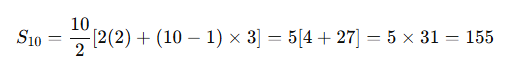
Sum = 155
Properties of an Arithmetic Sequence
- The difference between any two consecutive terms is constant.
- Every arithmetic sequence can be generated by repeatedly adding the common difference.
- The sequence grows linearly; hence, plotting its terms gives a straight line.
- The mean (average) of any two terms is equal to the middle term between them.
Arithmetic Mean
The Arithmetic Mean (A.M.) of two numbers a and b is defined as the average of both:
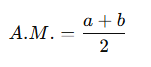
If three numbers form an arithmetic sequence, the middle number is the arithmetic mean of the other two.
Example 3:
Find the arithmetic mean between 8 and 20.
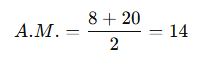
Arithmetic Mean = 14
Applications of Arithmetic Sequence
- Financial Planning: Predicting savings or installment payments.
- Physics: Calculating uniform motion or acceleration.
- Architecture: Designing patterns with equal spacing.
- Programming: Generating series or arrays with fixed intervals.
Arithmetic sequences describe linear growth models used in real-world problem solving.
The approach followed at E Lectures reflects both academic depth and easy-to-understand explanations.
People also ask:
An arithmetic sequence is a list of numbers that increases or decreases by the same value each time.
In an arithmetic sequence, terms change by addition; in a geometric sequence, terms change by multiplication.
It is the fixed value added to each term to get the next term.
It helps find any term in the sequence without listing all the previous terms.
Yes, if terms are decreasing, the common difference (d) is negative.