Arrays in C: Declaration, Initialization and Addressing

Learn arrays in C from zero, declare, initialize, index, compute sizes, and map 1D/2D addresses in row/column-major with worked examples.

What is an array?

An array is a data structure that stores a collection of elements of the same type in contiguous memory, accessed by an index. In C, indexing starts at 0.

Introduction to Data Structures 2025

Declaring arrays in C

Syntax: dataType arrayName[arraySize];
Example:

int myArray[5];   // 5 integers; values are uninitialized (garbage) in C

Notes:

• In C, array elements are not auto-initialized.
• Once declared, the size is fixed.

Initializing arrays & updating elements

You can initialize with a brace list:

int nums[5] = {1, 2, 3, 4, 5};
int nums2[] = {1, 2, 3, 4, 5}; // size inferred as 5

Update by index:

nums[2] = -1; // third element becomes -1
nums[4] = 0;  // fifth element becomes 0

Analysis of Algorithms – Example of Summing Natural Numbers

Key characteristics of arrays

• Homogeneous type: all elements share one type.
• Contiguous memory: enables predictable addressing.
• Fixed size (C/C++/Java) vs dynamic in some languages.
• Indexed access: constant-time lookups by index.

Advantages

• Efficient storage & retrieval due to contiguity.
• Random access: a[k] is O(1).
• Easy to sort/search with classic algorithms.
• Versatile base for stacks, queues, etc.
• Simple mental model for beginners.

Disadvantages

• Fixed size; resizing needs reallocation/copy.
• Insert/Delete costly (shifts).
• Homogeneous only (no mixed types).
• Some ops slower than hash tables/trees.

Computing array size (elements & bytes)

• #elements = (UpperBound – LowerBound) + 1
• Total size (bytes) = #elements × sizeOfElement

1D arrays: address formula + example

Let B = base address (start of the array), W = size of each element in bytes, k = index, L = lower bound (in C usually 0).
Address of a[k]:

a[k] = B + W * (k - L)

If L = 0, then a[k] = B + W * k.

Practice: 1D questions

Q1. Base B=250, each element W=3 bytes. Address of 5th element of a[10]?

• Indexing from 0 → 5th element is k=4.
• Address = 250 + 3 * 4 = 262.

Q2. A[-6…6], W=4 bytes, base B=3500. Address of A[0]?

• L=-6, k=0 → k - L = 6.
• Address = 3500 + 4 * 6 = 3524.

2D arrays: concept & use

A 2D array is an array of arrays, modeled as a matrix of rows and columns useful for tables and grid-like data.

Declaring/initializing 2D arrays

int disp[2][4] = {
  {10, 11, 12, 13},
  {14, 15, 16, 17}
};
// or (flattened initializer)
int disp2[2][4] = {10,11,12,13, 14,15,16,17};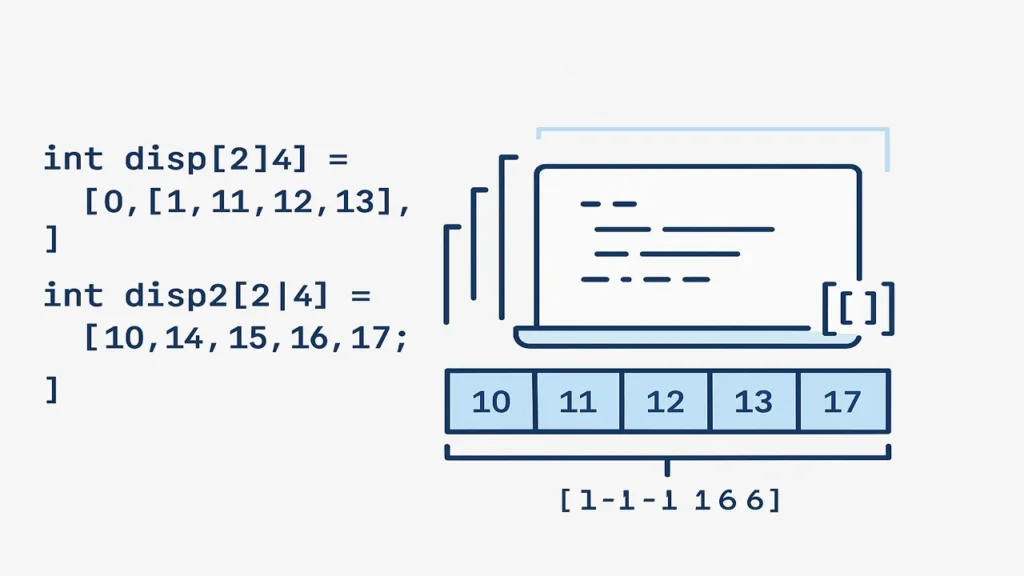

2D arrays in memory (overview)

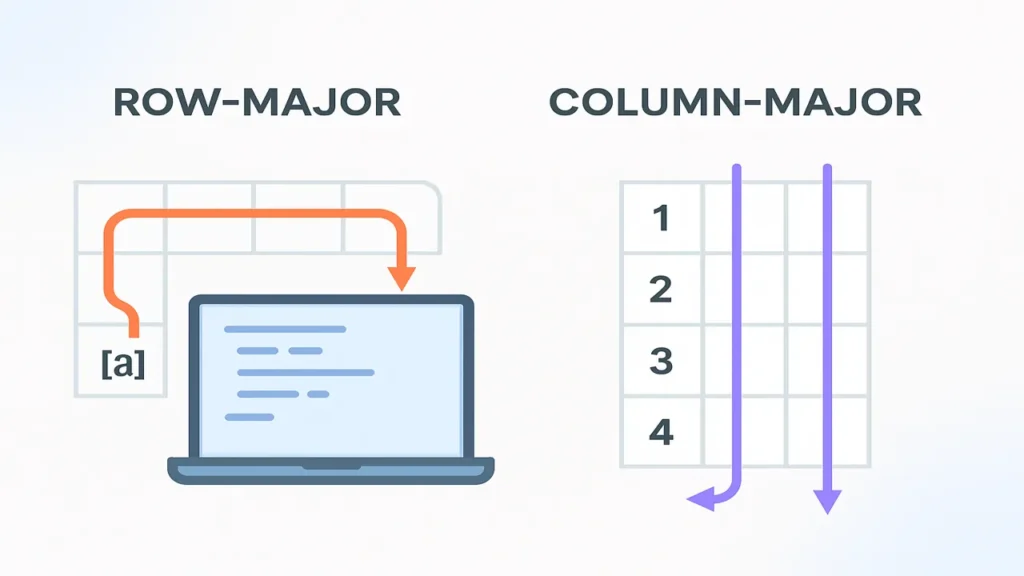
Multidimensional arrays are stored linearly in RAM. The order defines which elements are contiguous.
Row-major: rows are stored one after another (C uses row-major).
Column-major: columns are stored one after another.

Row-major vs column-major (intuition)

• Row-major: “finish the row, then move to next row.”
• Column-major: “finish the column, then move to next column.”

Row-major address formula (with meaning)

For a[i][j] with row bounds L1…U1, col bounds L2…U2:

Address = B + W * [ (U2 - L2 + 1) * (i - L1) + (j - L2) ]

Meaning:

• (U2 - L2 + 1) = #columns
• (i - L1) = rows before row i
• (j - L2) = offset inside row i

Column-major address formula (with meaning)

Address = B + W * [ (U1 - L1 + 1) * (j - L2) + (i - L1) ]

Meaning:

• (U1 - L1 + 1) = #rows
• (j - L2) = columns before column j
• (i - L1) = offset inside column j

Practice: 2D question (worked)

Given: VAL[1…15][1…10], W=4 bytes, B=1500. Find address of VAL[12][9]
Row-major (C style):

#cols = 10
i - L1 = 12 - 1 = 11
j - L2 = 9  - 1 = 8
Address = 1500 + 4 * (10*11 + 8)
        = 1500 + 4 * (110 + 8)
        = 1500 + 4 * 118
        = 1500 + 472
        = 1972

Column-major:

#rows = 15
j - L2 = 8
i - L1 = 11
Address = 1500 + 4 * (15*8 + 11)
        = 1500 + 4 * (120 + 11)
        = 1500 + 4 * 131
        = 1500 + 524
        = 2024

People also ask: