Sets in Mathematics Definition, Types & Examples

Sets in Mathematics explain how objects are grouped and related. Learn definitions, notations, types, and real-life examples with easy explanations.

Understanding Sets in Mathematics

A set is one of the most fundamental concepts in mathematics. It refers to a well-defined collection of distinct objects, considered as a single unit. These objects are called elements or members of the set. Sets are used to group numbers, symbols, or even real-world items for logical reasoning and data organization.

For example:
A = {1, 2, 3, 4, 5} is a set of natural numbers less than 6.
B = {red, blue, green} is a set of colors.

The study of sets forms the basis for modern mathematics, logic, and computer science.

Representation of Sets

There are two common methods to represent a set:

Roster (Tabular) Form

In this method, all elements are listed inside curly brackets { }, separated by commas.
Example:
A = {2, 4, 6, 8, 10} represents even numbers less than 11.

Set-builder Form

In this form, a condition defines the elements of the set.
Example:
A = {x | x is an even number less than 11}
Here, the vertical bar “|” means “such that.”

Types of Sets

Sets can be classified into several types depending on their elements:

Empty or Null Set (∅)

A set that contains no elements.
Example: A = {x | x < 0, x ∈ Natural numbers} → ∅

Finite Set

A set with a countable number of elements.
Example: A = {1, 3, 5, 7, 9}

Infinite Set

A set that has an uncountable number of elements.
Example: B = {x | x ∈ Natural numbers}

Equal Sets

Two sets are equal if they have exactly the same elements.
Example: A = {2, 4, 6} and B = {6, 4, 2} → A = B

Equivalent Sets

Sets having the same number of elements.
Example: A = {1, 2, 3} and B = {a, b, c}

Subset (⊆)

A set A is a subset of B if every element of A is also in B.
Example: A = {1, 2} is a subset of B = {1, 2, 3}.

Power Set (P)

The set of all subsets of a given set.
Example:
If A = {1, 2}, then
P(A) = {∅, {1}, {2}, {1,2}}

Universal Set (U)

A set that contains all the objects under consideration.
Example:
If U represents all natural numbers up to 10, then
U = {1,2,3,4,5,6,7,8,9,10}.

Set Operations

Sets can be combined and compared using specific operations:

Union (A ∪ B)

Elements belonging to either A or B.
Example:
A = {1,2,3} and B = {3,4,5}
→ A ∪ B = {1,2,3,4,5}

Intersection (A ∩ B)

Elements common to both A and B.
Example:
A ∩ B = {3}

Difference (A – B)

Elements in A but not in B.
Example:
A – B = {1,2}

Complement (A′)

All elements in the universal set U that are not in A.
Example:
If U = {1,2,3,4,5} and A = {2,4}, then A′ = {1,3,5}.

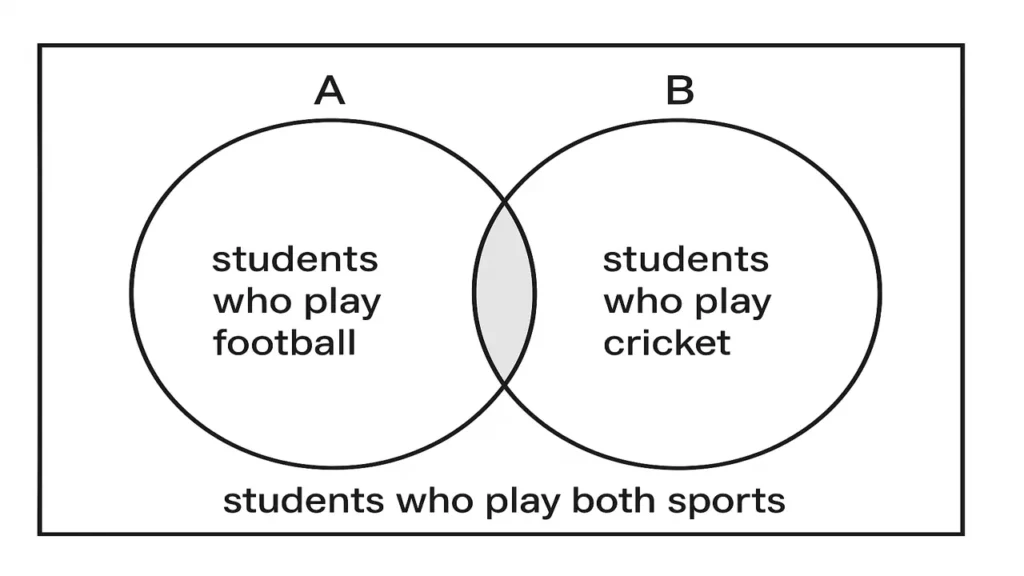
Venn Diagrams

Venn diagrams are visual tools used to represent sets and their relationships. Each set is shown as a circle within a rectangle representing the universal set. Overlapping areas show intersections, while separate regions show differences.

For example:
If A = students who play football and B = students who play cricket,
then A ∩ B = students who play both sports.

Real-Life Applications of Sets

• Data Classification: Grouping data (e.g., students by grades or blood type).
• Database Design: Used in SQL and data relationships.
• Logic and Programming: If–else conditions and Boolean algebra are based on set theory.
• Probability: Events in probability are treated as sets of outcomes.

Sets are not just theoretical they shape every logical system in computing and mathematics.

Important Symbols in Set Theory

Symbol	Meaning	Example
∈	Element of	3 ∈ {1,2,3}
∉	Not an element of	5 ∉ {1,2,3}
⊆	Subset	{1,2} ⊆ {1,2,3}
⊂	Proper subset	{1,2} ⊂ {1,2,3}
∪	Union	A ∪ B
∩	Intersection	A ∩ B
∅	Empty set	{}
U	Universal set	All elements considered
P(A)	Power set	All subsets of A

Summary

Concept	Meaning	Example
Set	Collection of distinct objects	{1,2,3}
Subset	Elements of one set belong to another	{1,2} ⊆ {1,2,3}
Union	Combination of all elements	A ∪ B
Intersection	Common elements	A ∩ B
Difference	Elements in one set but not another	A – B
Complement	Elements not in the set	A′

The approach followed at E Lectures reflects both academic depth and easy-to-understand explanations.

People also ask: