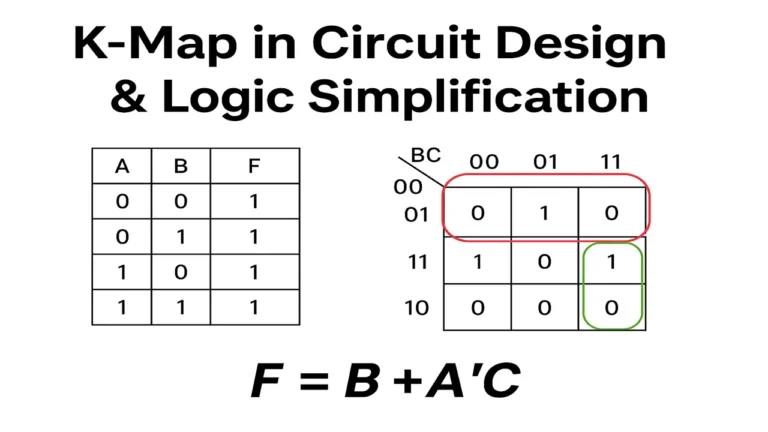
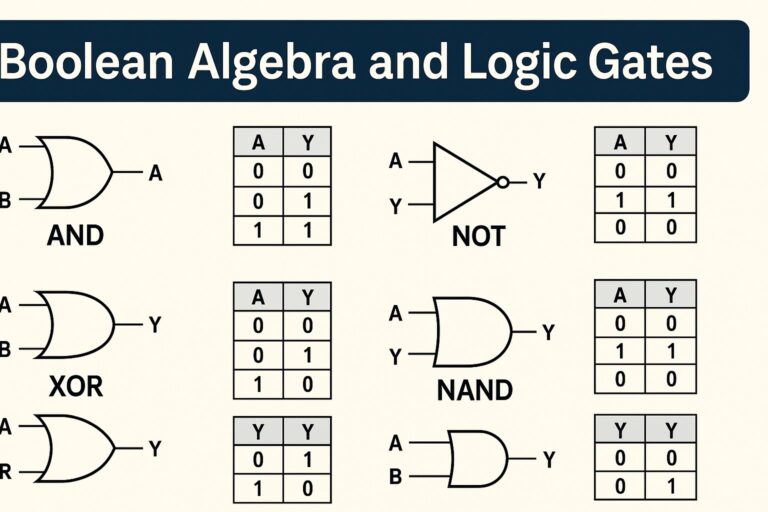
Digital Logic Design is the study of how electronic systems use 0s and 1s (binary numbers) to represent, process, and store information. It forms the foundation of all modern digital devices like computers, calculators, smartphones, and even Artificial Intelligence systems.
Key Points in the Definition of Digital Logic Design
“Digital” → means information is handled in discrete values (0 and 1), not continuous signals.
“Logic” → refers to using rules of reasoning (Boolean algebra & logic gates) to make decisions (true/false, yes/no).
“Design” → is about building circuits that perform tasks like addition, memory storage, comparisons, etc.
Number Systems in Digital Logic Design
What is a Number System?
A number system is simply a way of representing and expressing numbers using a set of symbols (digits) and a base (radix).
In Digital Logic Design, number systems are very important because all data inside computers and digital devices is stored and processed using these systems.
Binary System (Base 2)
- Digits: 0, 1
- The language of computers.
- Example: 1011 (1×2³ + 0×2² + 1×2¹ + 1×2⁰ = 11 in decimal).
Octal System (Base 8)
- Digits: 0–7
- Useful shorthand for binary (groups of 3 bits).
- Example: (725)₈ = 7×8² + 2×8¹ + 5×8⁰ = (469)₁₀.
Decimal System (Base 10)
- Digits: 0–9
- Everyday system humans use.
- Example: 548 (5×10² + 4×10¹ + 8×10⁰).
Hexadecimal System (Base 16)
- Digits: 0–9, A–F (A=10, B=11, … F=15).
- Very common in computer programming and memory addressing.
- Example: (2F)₁₆ = 2×16¹ + 15×16⁰ = (47)₁₀.
Representation of Number Systems
| Number System | Base (Radix) | Digits Used | Example Representation |
|---|---|---|---|
| Binary | 2 | 0, 1 | (1011)₂ = 1×2³ + 0×2² + 1×2¹ + 1×2⁰ = 11 |
| Octal | 8 | 0, 1, 2, 3, 4, 5, 6, 7 | (725)₈ = 7×8² + 2×8¹ + 5×8⁰ = 469 |
| Decimal | 10 | 0–9 | (452)₁₀ = 4×10² + 5×10¹ + 2×10⁰ |
| Hexa-decimal | 16 | 0–9, A–F (A=10, B=11 … F=15) | (2F)₁₆ = 2×16¹ + 15×16⁰ = 47 |

Conversion Between Number Systems
Digital systems don’t always use the same number system.
Why Conversions Matter in Digital Logic Design
- Bridge Between Humans and Machines
- We think in decimal, but computers process binary.
- Conversions allow smooth communication between user input and computer processing.
- Simplification of Binary Representation
- Long binary strings are hard to read.
- Converting to octal (groups of 3 bits) or hexadecimal (groups of 4 bits) makes representation shorter and easier.
- Example:
10111101₂→275₈orBD₁₆.
- Error Detection & Debugging
- Engineers use conversions to quickly analyze binary data in a human-friendly format (especially in programming, memory addresses, and circuit design).
- Efficient Data Representation
- Hexadecimal is widely used in machine code, assembly language, and memory addresses because it compresses long binary values into fewer digits.
- Learning Foundation for Advanced Topics
- Understanding conversions prepares students for Boolean algebra, logic circuits, microprocessors, and AI hardware systems.
Binary → Octal: Step-by-Step
Octal Conversion Table (3-bit Groups)
| Octal Digit | 4 | 2 | 1 | Binary (3-bit) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 000 |
| 1 | 0 | 0 | 1 | 001 |
| 2 | 0 | 1 | 0 | 010 |
| 3 | 0 | 1 | 1 | 011 |
| 4 | 1 | 0 | 0 | 100 |
| 5 | 1 | 0 | 1 | 101 |
| 6 | 1 | 1 | 0 | 110 |
| 7 | 1 | 1 | 1 | 111 |
- Write the binary number.
- Group bits in 3s from right to left. (e.g.,
1101011→1 101 011) - Pad the left group with leading zeros if it has fewer than 3 bits. (
1→001) - Replace each 3-bit group with one octal digit using the table below.
- Join the octal digits.
- Example: (
1101011)₂
Group:001 101 011→ Octal digits:1 5 3→(153)₈
2. Example: Convert (1010.1110)₂ → Octal
Step 1: Split into integer and fractional parts
- Integer part = 1010
- Fractional part = .1110
Step 2: Group in 3 bits
- For integer part (left side) → group from right to left
1010→001 010
- For fraction part (right side) → group from left to right
.1110→.111 000
Step 3: Convert each 3-bit group to Octal digit
001→ 1010→ 2111→ 7000→ 0
Step 4: Write the Octal number
So, (1010.1110)₂ = (12.70)₈Octal → Binary Conversion
👉 Rule: Replace each octal digit with its 3-bit binary equivalent (from the table we made earlier).
Octal → Binary: Step-by-Step
Example 1: Convert (572)₈ → Binary
Step 1: Write each digit separately
- 5 → 101
- 7 → 111
- 2 → 010
Step 2: Join them together
(572)₈ = 101 111 010₂
Answer: (572)₈=(101111010)₂
Example 2: Convert (12.70)₈ → Binary
Step 1: Split into integer and fraction parts
- Integer part = 12
- Fraction part = .70
Step 2: Convert each digit into 3-bit binary
- 1 → 001
- 2 → 010
- 7 → 111
- 0 → 000
Step 3: Join them together
Integer: 12 → 001 010
Fraction: .70 → .111 000
Step 4: Combine
(12.70)₈ = 001010.111000₂
Answer: (12.70)₈=(1010.1110)₂
Binary ↔ Hexadecimal
Since Hexa-Decimal is base-16, we use 4-bit groups (instead of 3 bits like Octal).
Hexadecimal Conversion Table (4-bit Groups)
| Hex Digit | 8 | 4 | 2 | 1 | Binary (4-bit) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0000 |
| 1 | 0 | 0 | 0 | 1 | 0001 |
| 2 | 0 | 0 | 1 | 0 | 0010 |
| 3 | 0 | 0 | 1 | 1 | 0011 |
| 4 | 0 | 1 | 0 | 0 | 0100 |
| 5 | 0 | 1 | 0 | 1 | 0101 |
| 6 | 0 | 1 | 1 | 0 | 0110 |
| 7 | 0 | 1 | 1 | 1 | 0111 |
| 8 | 1 | 0 | 0 | 0 | 1000 |
| 9 | 1 | 0 | 0 | 1 | 1001 |
| A (10) | 1 | 0 | 1 | 0 | 1010 |
| B (11) | 1 | 0 | 1 | 1 | 1011 |
| C (12) | 1 | 1 | 0 | 0 | 1100 |
| D (13) | 1 | 1 | 0 | 1 | 1101 |
| E (14) | 1 | 1 | 1 | 0 | 1110 |
| F (15) | 1 | 1 | 1 | 1 | 1111 |
Conversion Examples
Example 1: Binary → Hexadecimal
Convert (1010111101)₂ → Hexa- Decimal
Step 1: Group binary digits into 4 bits from right to left10 1011 1101 → pad left: 0010 1011 1101
Step 2: Replace each group using table
- 0010 → 2
- 1011 → B
- 1101 → D
Step 3: Write result
(1010111101)₂ = (2BD)₁₆
Example 2: Hexadecimal → Binary
Convert (3F.A)₁₆ → Binary
Step 1: Convert each digit separately
- 3 → 0011
- F → 1111
- A → 1010
Step 2: Combine
(3F.A)₁₆ = 00111111.1010₂
Answer: (3F.A)₁₆=(111111.1010)₂
Quick Rule Recap:
- Binary → Hex: Group in 4 bits (right for integer, left for fraction).
- Hex → Binary: Replace each hex digit with its 4-bit equivalent.
Octal ↔ Hexadecimal
Since Octal is base-8 and Hexadecimal is base-16, we can’t convert them directly by a single step — the best method is:
👉 Octal → Binary → Hex
👉 Hex → Binary → Octal
Example 1: Octal → Hexadecimal
Convert (756)₈ → Hexadecimal
Step 1: Convert Octal → Binary (each digit = 3 bits)
- 7 → 111
- 5 → 101
- 6 → 110
So, (756)₈ = 111101110₂
Step 2: Group Binary → Hex (4 bits per group)
111101110 → pad left: 0001 1110 1110
Step 3: Replace groups with Hex digits
- 0001 → 1
- 1110 → E
- 1110 → E
Answer: (756)₈=(1EE)₁₆
Example 2: Hexadecimal → Octal
Convert (2F)₁₆ → Octal
Step 1: Convert Hex → Binary (each digit = 4 bits)
- 2 → 0010
- F → 1111
So, (2F)₁₆ = 00101111₂
Step 2: Group Binary → Octal (3 bits per group)
00101111 → group as 000 101 111
Step 3: Replace groups with Octal digits
- 000 → 0
- 101 → 5
- 111 → 7
Answer: (2F)₁₆=(57)₈
Binary → Decimal
👉 Rule: Multiply each binary digit by 2n2^n2n (where n is the position, counting from right starting at 0) and then add them.
Example 1: Convert (110101)₂ → Decimal
Step 1: Write place values (110101)2=1×25+1×24+0×23+1×22+0×21+1×20(110101)_2 = 1×2^5 + 1×2^4 + 0×2^3 + 1×2^2 + 0×2^1 + 1×2^0(110101)2=1×25+1×24+0×23+1×22+0×21+1×20
Step 2: Calculate
= (32 + 16 + 0 + 4 + 0 + 1)
= 53
Answer: (110101)₂=(53)₁₀
Decimal → Binary
👉 Rule: Repeatedly divide by 2 and record the remainders. Write the remainders from bottom to top.
Example 2: Convert (53)₁₀ → Binary
Step 1: Divide by 2 until quotient = 0
| Division | Quotient | Remainder |
|---|---|---|
| 53 ÷ 2 | 26 | 1 |
| 26 ÷ 2 | 13 | 0 |
| 13 ÷ 2 | 6 | 1 |
| 6 ÷ 2 | 3 | 0 |
| 3 ÷ 2 | 1 | 1 |
| 1 ÷ 2 | 0 | 1 |
Step 2: Read remainders bottom → top
= 110101
Answer: (53)₁₀=(110101)₂
✨ Notice how both examples match: (110101)₂ ⟷ (53)₁₀
(110101)₂⟷(53)₁₀
Number System Conversion Summary
| From / To | Rule / Method | Example | Answer |
|---|---|---|---|
| Binary → Octal | Group binary digits into 3 bits (right to left for integer, left to right for fraction) | (1010.1110)₂ | (12.70)₈ |
| Octal → Binary | Replace each octal digit with its 3-bit binary equivalent | (572)₈ | (101111010)₂ |
| Binary → Hexadecimal | Group binary digits into 4 bits | (1010111101)₂ | (2BD)₁₆ |
| Hexadecimal → Binary | Replace each hex digit with its 4-bit binary equivalent | (3F.A)₁₆ | (111111.1010)₂ |
| Octal → Hexadecimal | Convert Octal → Binary (3 bits), then Binary → Hex (4 bits) | (756)₈ | (1EE)₁₆ |
| Hexadecimal → Octal | Convert Hex → Binary (4 bits), then Binary → Octal (3 bits) | (2F)₁₆ | (57)₈ |
| Binary → Decimal | Multiply each digit by 2n2^n2n and add | (110101)₂ | (53)₁₀ |
| Decimal → Binary | Repeated division by 2, record remainders bottom-to-top | (53)₁₀ | (110101)₂ |
Key Memory Tricks for Students
- Octal ↔ Binary = 3 bits
- Hex ↔ Binary = 4 bits
- Decimal ↔ Binary = Place value / Division by 2
- Octal ↔ Hex = Always convert through Binary
Number System Conversion Examples
Understanding conversions between number systems is essential in Digital Logic Design (DLD) and Computer Architecture. Let’s explore each conversion type with easy-to-follow examples.
Binary to Decimal Conversion
Example: Convert (1011)₂ to Decimal.
Step 1: Write binary digits with their positional values (powers of 2):
1 × 2³ + 0 × 2² + 1 × 2¹ + 1 × 2⁰
= 8 + 0 + 2 + 1
= 11 (Decimal)
Answer: (1011)₂ = (11)₁₀
Decimal to Binary Conversion
Example: Convert (25)₁₀ to Binary.
Step 1: Divide the number by 2 repeatedly and record remainders.
| Step | Division | Quotient | Remainder |
|---|---|---|---|
| 1 | 25 ÷ 2 | 12 | 1 |
| 2 | 12 ÷ 2 | 6 | 0 |
| 3 | 6 ÷ 2 | 3 | 0 |
| 4 | 3 ÷ 2 | 1 | 1 |
| 5 | 1 ÷ 2 | 0 | 1 |
Step 2: Write remainders from bottom to top → 11001
Answer: (25)₁₀ = (11001)₂
Octal to Decimal Conversion
Example: Convert (347)₈ to Decimal.
Step 1: Multiply each digit by powers of 8.
3 × 8² + 4 × 8¹ + 7 × 8⁰
= 3 × 64 + 4 × 8 + 7 × 1
= 192 + 32 + 7
= 231 (Decimal)
Answer: (347)₈ = (231)₁₀
Decimal to Octal Conversion
Example: Convert (125)₁₀ to Octal.
Step 1: Divide the number by 8 repeatedly and record remainders.
| Step | Division | Quotient | Remainder |
|---|---|---|---|
| 1 | 125 ÷ 8 | 15 | 5 |
| 2 | 15 ÷ 8 | 1 | 7 |
| 3 | 1 ÷ 8 | 0 | 1 |
Step 2: Write remainders from bottom to top → 175
Answer: (125)₁₀ = (175)₈
Hexadecimal to Decimal Conversion
Example: Convert (2F)₁₆ to Decimal.
Step 1: Write each hex digit with its decimal equivalent.
2 = 2, F = 15
2 × 16¹ + 15 × 16⁰
= 32 + 15
= 47 (Decimal)
Answer: (2F)₁₆ = (47)₁₀
Decimal to Hexadecimal Conversion
Example: Convert (125)₁₀ to Hexadecimal.
Step 1: Divide the number by 16 repeatedly.
| Step | Division | Quotient | Remainder |
|---|---|---|---|
| 1 | 125 ÷ 16 | 7 | 13 → D |
| 2 | 7 ÷ 16 | 0 | 7 |
Step 2: Write remainders from bottom to top → 7D
Answer: (125)₁₀ = (7D)₁₆
Summary Table of Examples
| Conversion | Example | Result |
|---|---|---|
| Binary → Decimal | (1011)₂ | (11)₁₀ |
| Decimal → Binary | (25)₁₀ | (11001)₂ |
| Octal → Decimal | (347)₈ | (231)₁₀ |
| Decimal → Octal | (125)₁₀ | (175)₈ |
| Hex → Decimal | (2F)₁₆ | (47)₁₀ |
| Decimal → Hex | (125)₁₀ | (7D)₁₆ |