K-Map in Circuit Design
Learn how K-Maps (Karnaugh Maps) are used in circuit design to simplify complex Boolean expressions into minimal logic gate implementations.
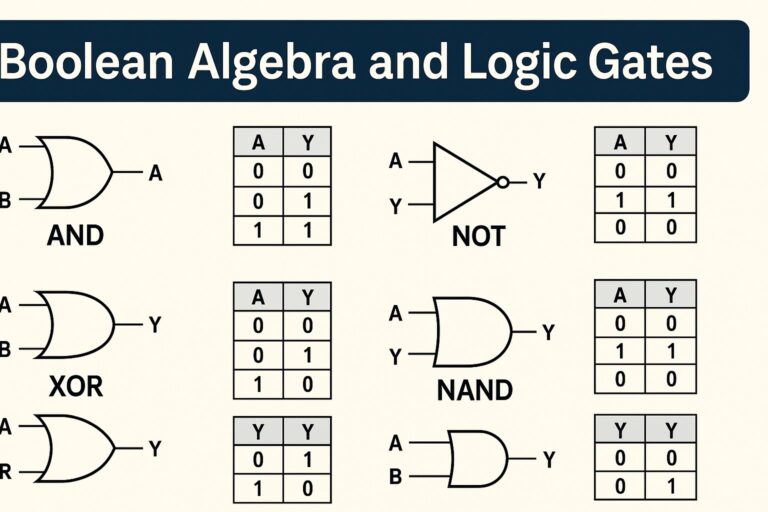
Logic Gates Summary
1. Basic Gates
These gates are the fundamental building blocks of digital circuits:
- AND: Y = A * B (or Y = AB)
- OR: Y = A + B.
- NOT: Y = A’
2. Universal Gates
These gates can be used to construct any of the other logic gates:
- NAND: Y = (A * B)’
- NOR: Y = (A + B)’
3. Arithmetic Gates
These gates are often used in arithmetic and comparison circuits:
- XOR (Exclusive-OR): Y = A B’ + A’ B (or A⊕B)
- X-NOR (Exclusive-NOR) Y = A B + A’ B’ (or A⊙B)

For More. Digital Logic Design (DLD) Foundation of Computing & AI
Sum of Products (SOP)
What Is SOP?
Sum of Products (SOP) is a standard way of expressing a Boolean function.
It means you write the logic expression as a sum (OR) of several product (AND) terms.
Each product term represents a condition where the output is 1 in the truth table.
So in simple words:
SOP = OR-ing of multiple AND terms.
F = AB’C+ABC’+ABC
Each term AB’C is called a minterm a combination of variables that make the output equal to 1.
How to Derive SOP from a Truth Table
Step 1: Write the truth table
Example for a function of three variables (A, B, C):
| A | B | C | Output (F) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
For More. Boolean Algebra and Logic Gates in Digital Logic Design 2025
Step 2: Identify rows where F = 1
→ Rows: 2, 4, 5, 7, 8 (in decimal form).
Step 3: Write corresponding minterms
For each row where output = 1, write an AND term:
- Row 2: A′B′C
- Row 4: A′BC
- Row 5: AB′C′
- Row 7: ABC’
- Row 8: ABC
Step 4: OR all minterms together
F= A′B′C + A′BC + AB′C′ + ABC’ + ABC
This is the canonical SOP expression.
Definition of Canonical Form
In Boolean algebra, a canonical form (also called standard form) is a way of writing a Boolean expression where each term includes all the variables in the system, either in complemented (0) or uncomplemented (1) form.
Canonical form = every term has all input variables once.
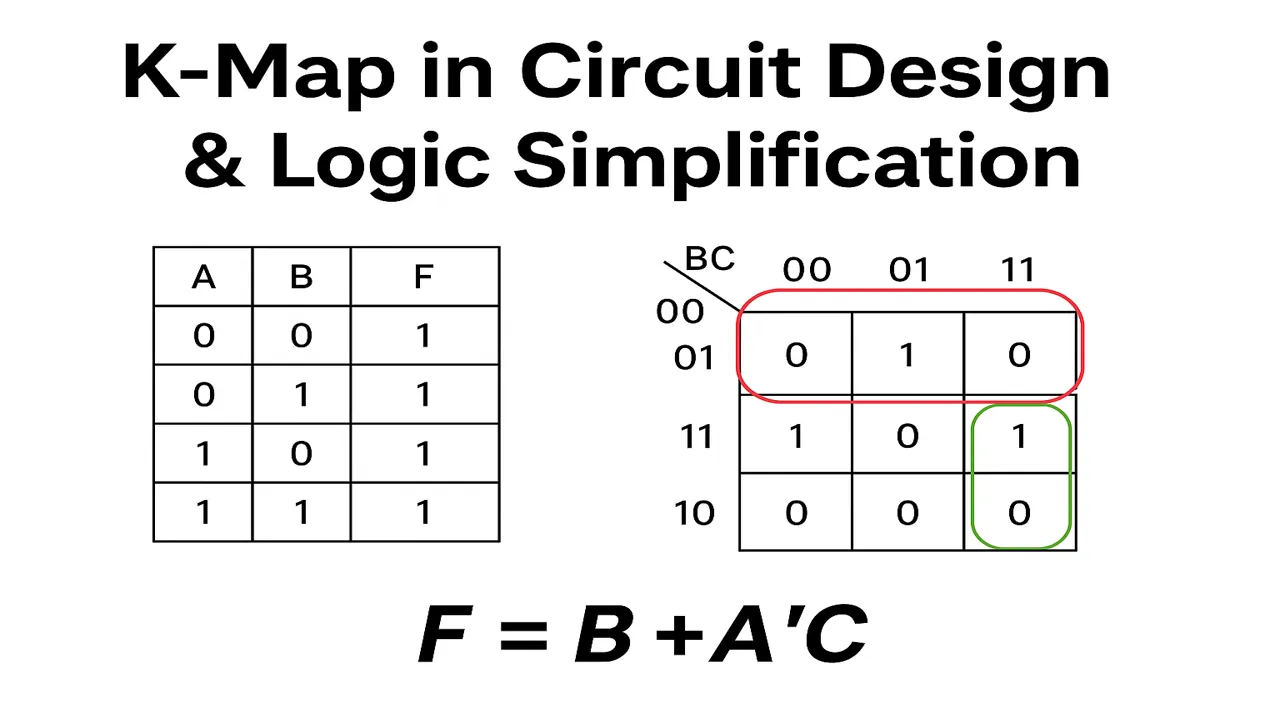
Karnaugh Map (K-Map) From Truth Table to Simplified Logic
Why is K-Map Required?
When we write a Boolean function directly from a truth table, we usually get a long Sum of Products (SOP) expression.
Simplifying this manually using Boolean algebra can be:
- Time-consuming
- Prone to human error
- Hard to visualize for many variables
K-Map (Karnaugh Map) solves this problem by providing a visual method to simplify Boolean expressions quickly and accurately.
It lets you group together adjacent 1’s in the truth table to eliminate unnecessary variables and get the minimum SOP or POS form.
Explaining Gray Code
Gray Code (Reflected Binary Code) is the special ordering used for labeling the rows and columns of a K-map.
- Definition: Gray code is a sequence of binary numbers where only one bit changes between any two successive values.
- Purpose in K-Maps: This rule is crucial because the core principle of K-map grouping is combining adjacent terms that differ by only one variable. By using Gray code to label the map, any physically adjacent cells (including wrap-around cells) are logically adjacent (differ by one bit), which ensures valid simplification groups.
| Decimal | Standard Binary | Gray Code |
| 0 | 00 | 00 |
| 1 | 01 | 01 |
| 2 | 10 | 11 |
| 3 | 11 | 10 |
| Notice the change between 01 and 11 is only the first bit, and between 11 and 10 is only the last bit. |
K-Map Structures by Variable Count
The K-map must have $2^n$ cells, where $n$ is the number of variables.
2-Variable K-Map
This map is structured as 2 X 2. Gray code is applied to both A and B.
| A\B | 0 | 1 |
|---|---|---|
| 0 | F(0,0) | F(0,1) |
| 1 | F(1,0) | F(1,1) |
Example
| A | B | F |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Plot K-Map:
| A\B | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Grouping: combine adjacent 1’s
Minimal SOP: F=A+B
3-Variable K-Map (A, B, C)
| A∖BC | 00 (B′C′) | 01 (B′C) | 11 (BC) | 10 (BC′) |
|---|---|---|---|---|
| 0 (A′) | m₀ | m₁ | m₃ | m₂ |
| 1 (A) | m₄ | m₅ | m₇ | m₆ |
Notice the column order: 00, 01, 11, 10 (Gray code: m3 and m2 are swapped from standard binary order).
How to Read This Table
Each cell corresponds to a minterm (m)Example Function
Let’s take: F(A,B,C)=∑m(1,2,3,5,7)
That means the function equals 1 for minterms m₁, m₂, m₃, m₅, m₇. a unique combination of A, B, and C values that produce one product term in Boolean logic.
For example:
- m₀ = A′B′C′ → A=0, B=0, C=0
- m₁ = A′B′C → A=0, B=0, C=1
- m₂ = A′BC′ → A=0, B=1, C=0
- m₃ = A′BC → A=0, B=1, C=1
- m₄ = AB′C′ → A=1, B=0, C=0
- m₅ = AB′C → A=1, B=0, C=1
- m₆ = ABC′ → A=1, B=1, C=0
- m₇ = ABC → A=1, B=1, C=1
Example Function
Let’s take: F(A,B,C)=∑m(1,2,3,5,7)
That means the function equals 1 for minterms m₁, m₂, m₃, m₅, m₇.
Plot in K-Map
| A∖BC | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 0 (A′) | 0 | 1 | 1 | 1 |
| 1 (A) | 0 | 1 | 1 | 0 |
let’s simplify
F= A′B′C + A′BC + AB′C + ABC + A′BC′
Boolean-algebra simplification
Group the four terms that share C:
F=(A′B′C+A′BC+AB′C+ABC)+A′BC′
=[(A′B′+A′B+AB′+AB)]C+A′BC′
=[A′(B′+B)+A(B′+B)]C+A′BC′
=(A′+A)C+A′BC′
=C+A′BC′.
Grouping:
- A 4-cell group covering m1,m3,m5,m7 (the entire C=1) → term C.
- A 2-cell group covering m2 with adjacent m3 → term A′B.
Result: F=C+A′B
4-Variable K-Map (A, B, C, D)
| AB\CD | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | m0 | m1 | m3 | m2 |
| 01 | m4 | m5 | m7 | m6 |
| 11 | m12 | m13 | m15 | m14 |
| 10 | m8 | m9 | m11 | m10 |
Example:
F(A,B,C,D)=∑m(0,2,5,7,8,9,10,14)
Plotting the K-Map
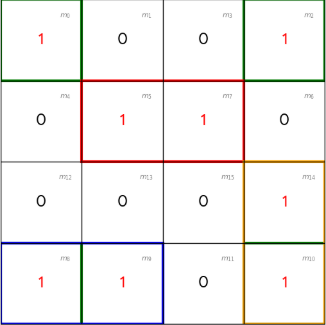
K-Map groupings (maximize size, allow wrapping)
- Quad: {m0,m2,m8,m10} (rows AB=00 & 10, cols CD=00 & 10)
- Common: B’ and D’ → term: B’ D’
- Pair (row 01, horizontal): {m5,m7}(CD = 01 & 11)
- Common: A’, B, D→ term: A’ B D
- Pair (row 10, horizontal): {m8,m9}(CD = 00 & 01)
- Common: A, B’, C’ → term: A B’ C’
- Pair (column 10, vertical): {m10,m14}(AB = 10 & 11)
- Common: A, C, D’→ term: A C D’
All 1’s are covered; no uncovered minterms remain.

- Quad (Corners) – Green: m0,m2,m8,m10 is still a valid Quad. B′D′
- Pair – Red: m5,m7 is still a valid Pair. A′BD
- Pair – Blue: m8,m9 is still a valid Pair. AB′C′ (Covers m9, m8 is redundant)
- Pair – Orange: m10,m14 (Vertical Wrap) is still a valid Pair. ACD′ (Covers m14, m10 is redundant)
Minimal SOP Expression
The following prime implicants form the minimal cover for all the minterms:
- Four Corners: Covers m0,m2,m8,m10.
- Term: B′D′
- Pair: Covers m5,m7.
- Term: A′BD
- Pair: Covers m8,m9. (Needed to uniquely cover m9)
- Term: AB′C′
- Pair (Vertical Wrap): Covers m10,m14. (Needed to uniquely cover m14)
- Term: ACD′
The minimal Sum of Products (SOP) expression is the logical OR of these terms:
F(A,B,C,D)=B′D′+A′BD+AB′C′+ACD′